Explanation:
The time dilation formula is given by
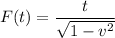
where t is the time measured by the moving observer and F(t) is the time measured by the stationary earth-bound observer and v is the velocity of the moving observer expressed as a fraction of the speed of light.
a) If the observer is moving at 80% of the speed of light and observes an event that lasts for 1 second, a stationary observer will see the same event occurring over a time period of
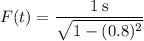
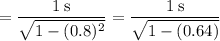
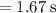
This means that any event observed by this moving observer will be seen by a stationary observer to occur 67% longer.
b) Given:
t = 1 second
F(t) = 2 seconds
We need to find the speed of the observer such that an event seen by this observer will occur twice as long as seen by a stationary observer. Move the term containing the radical to the left side so the equation becomes
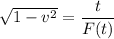
Take the square of both sides, we get
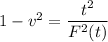
Solving for v, we get
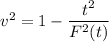
or
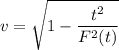
Putting in the values for t and F(t) we get
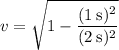
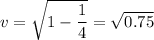
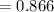
This means that the observer must moves at 86.6% of the speed of light.