Answer:
K = 2 10⁻⁸ J
Step-by-step explanation:
Let's solve this exercise in parts, we start by finding the charge on each plate of the capacitor
C = Q / ΔV
C = ε₀ A / d
ε₀ A / d = Q / ΔV
Q = ε₀ A ΔV / d (1)
indicate the potential difference ΔV₁ = 12 V, the distance between the plates d₁ = 3 mm = 0.003 m,
as the power supply is disconnected and the capacitor is ideal the charge remains constant
in the second part we separate the plates at d₂ = 5 mm = 0.005 m, using equation 1
ΔV₂ =
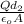
we substitute the equation for Q
ΔV₂ =
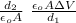
ΔV₂ =
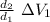
in the third part we use the concepts of energy
starting point. Test charge near positive plate
Em₀ = U = q ΔV₂
final point. Test charge near negative plate
Em_f = K
energy is conserved
Em₀ = Em_f
q ΔV₂ = K
K = q ΔV₁
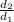
we calculate
K = 1 10⁻⁹ 12 0.005/0.003
K = 2 10⁻⁸ J