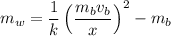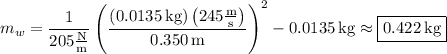Question

A bullet with a mass mb=13.5 g is fired into a block of wood at velocity vb=245 m/s. The block is attached to a spring that has a spring constant k of 205 N/m. The block and bullet continue to move, compressing the spring by 35.0 cm before the whole system momentarily comes to a stop. Assuming that the surface on which the block is resting is frictionless, determine the mass mw of the wooden block.

Answer 1

Momentum is conserved, so the sum of the momenta of the bullet and block before collision is equal to the momentum of the combined bullet-block system,

`m_bv_b+m_wv_w = (m_b+m_w)v`

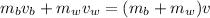
where v is the speed of the bullet-block system. The block starts at rest so it has no initial momentum, and solving for v gives

`v = (m_b)/(m_b+m_w) v_b`

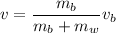
The total work W performed by the spring on the bullet-block system as it is compressed a distance x is

`W = -\frac12kx^2`

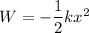
where k is the spring constant, and the work done is negative because the restoring force of the spring opposes the bullet-block as it compresses the spring.

By the work-energy theorem, the total work done is equal to the change in the bullet-block's kinetic energy ∆K, so we have

`W_(\rm total) = W = \Delta K`

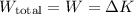
The bullet-block starts moving with velocity v found earlier and comes to a stop as the spring slows it down, so we have

`-\frac12kx^2 = -\frac12(m_b+m_w)v^2 \implies kx^2 = \frac{{m_b}^2}{m_b+m_w}{v_b}^2`

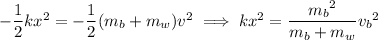
Solve for
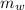`m_w`:

`m_w=\frac1k\left(\frac{m_bv_b}x\right)^2-m_b`

`m_w=\frac1{205(\rm N)/(\rm m)}\left(\frac{(0.0135\,\mathrm{kg})\left(245(\rm m)/(\rm s)\right)}{0.350\,\rm m}\right)^2-0.0135\,\mathrm{kg}\approx \boxed{0.422\,\mathrm{kg}}`