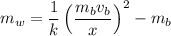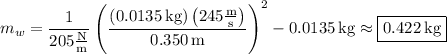Momentum is conserved, so the sum of the momenta of the bullet and block before collision is equal to the momentum of the combined bullet-block system,
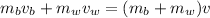
where v is the speed of the bullet-block system. The block starts at rest so it has no initial momentum, and solving for v gives
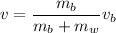
The total work W performed by the spring on the bullet-block system as it is compressed a distance x is
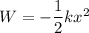
where k is the spring constant, and the work done is negative because the restoring force of the spring opposes the bullet-block as it compresses the spring.
By the work-energy theorem, the total work done is equal to the change in the bullet-block's kinetic energy ∆K, so we have

The bullet-block starts moving with velocity v found earlier and comes to a stop as the spring slows it down, so we have
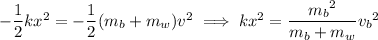
Solve for
 :
: