Answer:
Step-by-step explanation:
From the given information:
weight of fiber
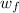 = 3.0 g
= 3.0 g
weight of composite specimen
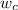 = 4.0 g
= 4.0 g
specimen composite weight in water
 = 2.0 g
= 2.0 g
specific gravity of fiber
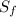 = 2.4
= 2.4
specific gravity of matrix
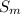 = 1.3
= 1.3
The weight of the matrix = weight of the composite - the weight of fiber
⇒ (4.0 - 3.0) g
= 1.0 g
The theoretical density of the composite
 can be determined by using the formula:
can be determined by using the formula:


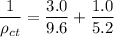
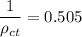
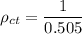
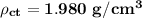
The experimental density
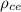 is determined by using the equation:
is determined by using the equation:
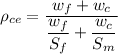
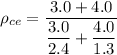
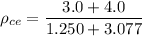
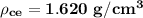
The void fraction is:
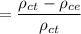
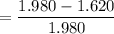
= 0.1818