Answer:
a) Irreversible, b) Reversible, c) Irreversible, d) Impossible.
Step-by-step explanation:
Maximum theoretical efficiency for a power cycle (
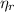 ), no unit, is modelled after the Carnot Cycle, which represents a reversible thermodynamic process:
), no unit, is modelled after the Carnot Cycle, which represents a reversible thermodynamic process:
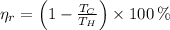 (1)
(1)
Where:
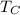 - Temperature of the cold reservoir, in Kelvin.
- Temperature of the cold reservoir, in Kelvin.
 - Temperature of the hot reservoir, in Kelvin.
- Temperature of the hot reservoir, in Kelvin.
The maximum theoretical efficiency associated with this power cycle is: (
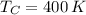 ,
,
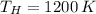 )
)
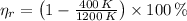

In exchange, real efficiency for a power cycle (
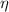 ), no unit, is defined by this expression:
), no unit, is defined by this expression:
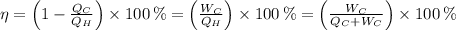 (2)
(2)
Where:
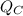 - Heat released to cold reservoir, in kilojoules.
- Heat released to cold reservoir, in kilojoules.
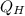 - Heat gained from hot reservoir, in kilojoules.
- Heat gained from hot reservoir, in kilojoules.
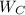 - Power generated within power cycle, in kilojoules.
- Power generated within power cycle, in kilojoules.
A power cycle operates irreversibly for
 , reversibily for
, reversibily for
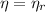 and it is impossible for
and it is impossible for
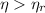 .
.
Now we proceed to solve for each case:
a)
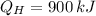 ,
,
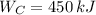
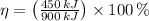

Since
 , the power cycle operates irreversibly.
, the power cycle operates irreversibly.
b)
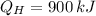 ,
,
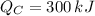
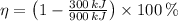
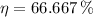
Since
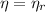 , the power cycle operates reversibly.
, the power cycle operates reversibly.
c)
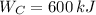 ,
,
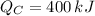
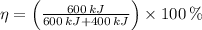
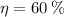
Since
 , the power cycle operates irreversibly.
, the power cycle operates irreversibly.
d) Since
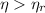 , the power cycle is impossible.
, the power cycle is impossible.