Question

A pendulum is constructed from a 6 kg mass attached to a strong cord of length 1.7 m also attached to a ceiling. Originally hanging vertically, the mass is pulled aside a small distance of 7.6 cm and released from rest. While the mass is swinging the cord exerts an almost-constant force on it. For this problem, assume the force is constant as the mass swings. How much work in J does the cord do to the mass as the mass swings a distance of 8.0 cm

Answer 1

work done is -2.8 × 10⁻⁶ J

Step-by-step explanation:

Given the data in the question;

mass of the pendulum m = 6 kg

Length of core = 1.7 m

Now, case1, mass is pulled aside a small distance of 7.6 cm and released from rest. so let θ₁ be the angle made by mass with vertical axis.

so, θ₁ = ( 7.6 × 10⁻² m / 1.7 m ) = 0.045 rad

In case2, mass is pulled aside a small distance of 8 cm and released from rest. so let θ₁ be the angle made by mass with vertical axis.

so, θ₂ = ( 8 × 10⁻² m / 1.7 m ) = 0.047 rad.

Now, the required work done will be;

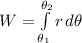
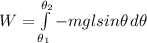
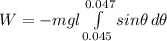
`W = \int\limits^(\theta_2) _(\theta_1) {r} \, d\theta`

`W = \int\limits^(\theta_2) _(\theta_1) {-mgl sin\theta } \, d\theta`

`W = -mgl \int\limits^(0.047 ) _(0.045 ) {sin\theta } \, d\theta`

W =
`-mgl[` -cosθ
`]^(0.047)_(0.045 )`

W = 6 × 9.8 × 1.7 × [ cos( 0.047 ) - cos( 0.045 ) ]

W = 6 × 9.8 × 1.7 × [ -2.8 × 10⁻⁸ ]

W = -2.8 × 10⁻⁶ J

Therefore, work done is -2.8 × 10⁻⁶ J