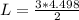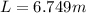Answer:
a)
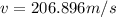
b)
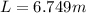
Step-by-step explanation:
From the question we are told that:
Frequency

Length
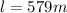
Total Mass
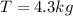
Tension
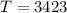
a)
Generally the equation for velocity is mathematically given by
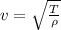
Where

Therefore
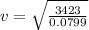
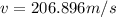
b)
Generally the equation for length of string is mathematically given by
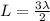
Where
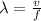
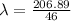
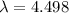
Therefore