Question

A particle makes 800 revolution in 4 minutes of a circle of 5cm. Find

i. it's period
ii. Angular Velocity
iii. Linear Velocity
iv. It's acceleration
PLEASE FORMULAE SHOULD BE WRITTEN CLEARLY.
YOU CAN SNAP AND SEND

Answer 1

i) The period of the particle is 0.3 seconds

ii) The angular velocity is approximately 20.94 rad/s

iii) The linear velocity is approximately 1.047 m/s

iv) The centripetal acceleration is approximately 6.98 m/s²

Step-by-step explanation:

The given parameters are;

The number of revolution of the particle, n = 800 revolution

The time it takes the particle to make 800 revolutions = 4 minutes

The dimension of the circle = 5 cm = 0.05 m

Given that the dimension of the circle is the radius of the circle, we have;

i) The period of the particle, T = The time to complete one revolution

T = 1/(The number of revolutions per second)

∴ T = 1/(800 rev/(4 min × 60 s/min)) = 3/10 s

The period, T = 3/10 seconds = 0.3 seconds

ii) The angular velocity, ω = Angle covered/(Time)

800 revolutions in 4 minutes = Angle of (800 × 2·π) in 4 minutes

∴ ω = (800 × 2·π)/(4 × 60) = 20·π/3

The angular velocity, ω = 20·π/3 rad/s ≈ 20.94 rad/s

iii) The linear velocity, v = r × ω

∴ The linear velocity, v = 0.05 m × 20·π/3 rad/s = π/3 m/s ≈ 1.047 m/s

iv) The centripetal acceleration,
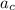`a_c` = v²/r

∴ The centripetal acceleration,
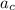`a_c` = (π/3)²/(0.05) = 20·π/9

The centripetal acceleration,
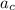`a_c` = 20·π/9 m/s² ≈ 6.98 m/s²