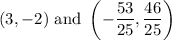Answer:
Our two intersection points are:
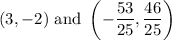
Explanation:
We want to find where the two graphs given by the equations:
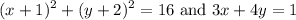
Intersect.
When they intersect, their x- and y-values are equivalent. So, we can solve one equation for y and substitute it into the other and solve for x.
Since the linear equation is easier to solve, solve it for y:
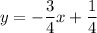
Substitute this into the first equation:
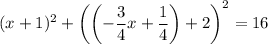
Simplify:

Square. We can use the perfect square trinomial pattern:
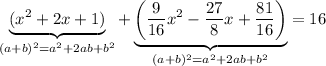
Multiply both sides by 16:
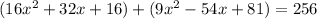
Combine like terms:
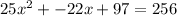
Isolate the equation:
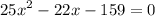
We can use the quadratic formula:
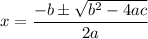
In this case, a = 25, b = -22, and c = -159. Substitute:

Evaluate:
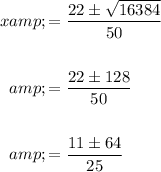
Hence, our two solutions are:
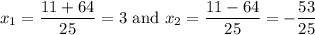
We have our two x-coordinates.
To find the y-coordinates, we can simply substitute it into the linear equation and evaluate. Thus:

And:
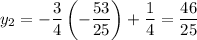
Thus, our two intersection points are: