Question

Find the exact value of tan(165°) using a difference of two angles

Answer 1

Answer:
`-2+√(3)`

=========================================================

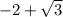
Work Shown:

Apply the following trig identity

`\tan(A - B) = (\tan(A)-\tan(B))/(1+\tan(A)*\tan(B))\\\\\tan(225 - 60) = (\tan(225)-\tan(60))/(1+\tan(225)*\tan(60))\\\\\tan(165) = (1-√(3))/(1+1*√(3))\\\\\tan(165) = (1-√(3))/(1+√(3))\\\\`

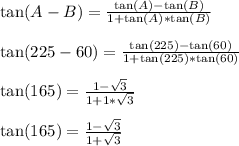
Now let's rationalize the denominator

`\tan(165) = (1-√(3))/(1+√(3))\\\\\tan(165) = ((1-√(3))(1-√(3)))/((1+√(3))(1-√(3)))\\\\\tan(165) = ((1-√(3))^2)/((1)^2-(√(3))^2)\\\\\tan(165) = ((1)^2-2*1*√(3)+(√(3))^2)/((1)^2-(√(3))^2)\\\\\tan(165) = (1-2√(3)+3)/(1-3)\\\\\tan(165) = (4-2√(3))/(-2)\\\\\tan(165) = -2+√(3)\\\\`

----------------------

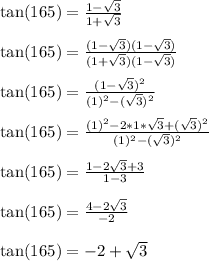
As confirmation, you can use the idea that if x = y, then x-y = 0. We'll have x = tan(165) and y = -2+sqrt(3). When computing x-y, your calculator should get fairly close to 0, if not get 0 itself.

Or you can note how

`\tan(165) \approx -0.267949\\\\-2+√(3) \approx -0.267949`

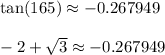
which helps us see that they are the same thing.

Further confirmation comes from WolframAlpha (see attached image). They decided to write the answer as
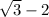`√(3)-2` but it's the same as above.