Answer:
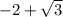
=========================================================
Work Shown:
Apply the following trig identity
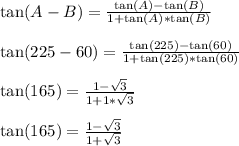
Now let's rationalize the denominator
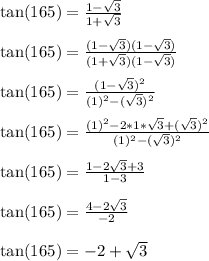
----------------------
As confirmation, you can use the idea that if x = y, then x-y = 0. We'll have x = tan(165) and y = -2+sqrt(3). When computing x-y, your calculator should get fairly close to 0, if not get 0 itself.
Or you can note how
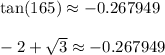
which helps us see that they are the same thing.
Further confirmation comes from WolframAlpha (see attached image). They decided to write the answer as
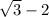 but it's the same as above.
but it's the same as above.