Answer:
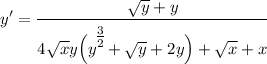
General Formulas and Concepts:
Calculus
Differentiation
- Derivatives
- Derivative Notation
Derivative Property [Multiplied Constant]:
![\displaystyle (d)/(dx) [cf(x)] = c \cdot f'(x)](https://img.qammunity.org/2022/formulas/mathematics/high-school/rwpyhrof52dro5d128gleq5obchnuu5qkj.png)
Derivative Property [Addition/Subtraction]:
![\displaystyle (d)/(dx)[f(x) + g(x)] = (d)/(dx)[f(x)] + (d)/(dx)[g(x)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/i90hl6t3gcguvrecodn8t9gnodav0w5ns8.png)
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Derivative Rule [Quotient Rule]:
![\displaystyle (d)/(dx) [(f(x))/(g(x)) ]=(g(x)f'(x)-g'(x)f(x))/(g^2(x))](https://img.qammunity.org/2022/formulas/mathematics/high-school/hrfl3gpx3dh352g7a9uj6guyxz9uxwhvl3.png)
Derivative Rule [Chain Rule]:
![\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)](https://img.qammunity.org/2022/formulas/mathematics/high-school/vue68srn3fe6bds4idxorm97z7tgwelamw.png)
Implicit Differentiation
Explanation:
Step 1: Define
Identify
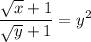
Step 2: Differentiate
- Implicit Differentiation:
![\displaystyle (dy)/(dx) \bigg[ (√(x) + 1)/(√(y) + 1) \bigg] = (dy)/(dx)[ y^2]](https://img.qammunity.org/2022/formulas/mathematics/college/bjumv7fv5dsvd7c5gq8la4td20uxdsfqsb.png)
- Quotient Rule:
![\displaystyle ((√(x) + 1)'(√(y) + 1) - (√(y) + 1)'(√(x) + 1))/((√(y) + 1)^2) = (dy)/(dx)[ y^2]](https://img.qammunity.org/2022/formulas/mathematics/college/7mtsxtgaano1kj0a1mh38xvamf6veyx5sw.png)
- Rewrite:
![\displaystyle \frac{(x^\Big{(1)/(2)} + 1)'(y^\Big{(1)/(2)} + 1) - (y^\Big{(1)/(2)} + 1)'(x^\Big{(1)/(2)} + 1)}{(y^\Big{(1)/(2)} + 1)^2} = (dy)/(dx)[ y^2]](https://img.qammunity.org/2022/formulas/mathematics/college/b83glqkhti89m722sc62l65rnk1nm2oxqt.png)
- Basic Power Rule [Addition/Subtraction, Chain Rule]:
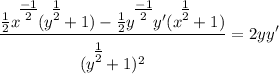
- Factor:
![\displaystyle \frac{(1)/(2) \bigg[ x^\Big{(-1)/(2)}(y^\Big{(1)/(2)} + 1) - y^\Big{(-1)/(2)}y'(x^\Big{(1)/(2)} + 1) \bigg] }{(y^\Big{(1)/(2)} + 1)^2} = 2yy'](https://img.qammunity.org/2022/formulas/mathematics/college/rt8imtcnr4j5jg3k28c7uxm86ebfew51qm.png)
- Rewrite:
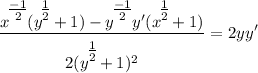
- Rewrite:
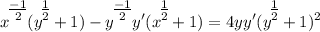
- Isolate y' terms:
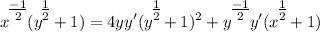
- Factor:
![\displaystyle x^\Big{(-1)/(2)}(y^\Big{(1)/(2)} + 1) = y' \bigg[ 4y(y^\Big{(1)/(2)} + 1)^2 + y^\Big{(-1)/(2)}(x^\Big{(1)/(2)} + 1)} \bigg]](https://img.qammunity.org/2022/formulas/mathematics/college/4jiiliv575dagtxcjhki1oge0l3fp348jm.png)
- Isolate y':
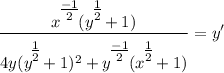
- Rewrite/Simplify:
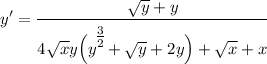
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Differentiation
Book: College Calculus 10e