Given:
The five number summary of two data sets are given as:
a) 0, 4, 12, 14, 20
b) 2, 8, 14, 18, 20
To find:
The range for the outliers.
Solution:
We know that,
An observation is considered an outlier if it is below

An observation is considered an outlier if it is above
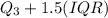
Where, IQR is the interquartile range and
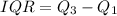 .
.
The five number summary of two data sets are given as:
0, 4, 12, 14, 20
Here,
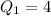 and
and
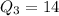 .
.
Now,
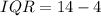
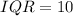
The range for the outliers is:
![[Q_1-1.5(IQR),Q_3+1.5(IQR)]=[4-1.5(10),14+1.5(10)]](https://img.qammunity.org/2022/formulas/mathematics/college/sawyzt5ts36uw8zgi5y3w28pbsrn29d8my.png)
![[Q_1-1.5(IQR),Q_3+1.5(IQR)]=[4-15,14+15]](https://img.qammunity.org/2022/formulas/mathematics/college/geisdu9rnu2uuuvm6xtv47d5s6fvh4m6oc.png)
![[Q_1-1.5(IQR),Q_3+1.5(IQR)]=[-11,29]](https://img.qammunity.org/2022/formulas/mathematics/college/fstjesgvwsas1pbiptm6s7v1jwng0iovww.png)
An observation is considered an outlier if it is below -11.
An observation is considered an outlier if it is above 29.
The five number summary of two data sets are given as:
2, 8, 14, 18, 20
Here,
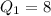 and
and
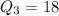 .
.
Now,
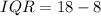
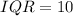
The range for the outliers is:
![[Q_1-1.5(IQR),Q_3+1.5(IQR)]=[8-1.5(10),18+1.5(10)]](https://img.qammunity.org/2022/formulas/mathematics/college/slh5zfyy4akcu9week725el96wszhbrcmi.png)
![[Q_1-1.5(IQR),Q_3+1.5(IQR)]=[8-15,18+15]](https://img.qammunity.org/2022/formulas/mathematics/college/8z88jjorqevv3jr8l39ex26xv3f3dqnron.png)
![[Q_1-1.5(IQR),Q_3+1.5(IQR)]=[-7,33]](https://img.qammunity.org/2022/formulas/mathematics/college/ix0pdwc8935g73j0abld49xomi11731mec.png)
An observation is considered an outlier if it is below -7.
An observation is considered an outlier if it is above 33.