Question

Last one! 50 points!​

Answer 1

Given that :

`\frak {\cos( \theta_(1) ) = - (13)/(15) }`

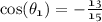
To find :

`\frak{ sin( \theta_(1) )}`

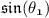
We know that cos θ is base/hypotentuse

So, here the base is -13 and the hypotentuse is 15

As we got the base and hypotentuse, perpendicular needs to be found out

Now, applying Pythagoras Theorem

According to Pythagoras theorem we know that :

• (Hypotentuse)² = (Base)² + (Perpendicular)²

Let us assume perpendicular be x

Putting the values we get

• (15)² = (-13)² + (x)²

• 225 = 169 + x²

By transposing we get

• x² = 225 - 169

• x = √56

• x = 2√14

sin θ formula : Perpendicular/Hypotentuse

`\star \: \: \underline{ \overline{ \boxed{ \frak{ sin (\theta_(1))} = (-2 √(14) )/(15) }}}`

Hence, the answer is -2√14/15

Answer 2

sin theta = -2 sqrt(14)/15

Explanation:

cos theta = adj / hyp

We can find the opp side by using the Pythagorean theorem

adj ^2 + opp ^2 = hyp^2

(-13)^2 + opp ^2 = 15^2

169 + opp ^2 = 225

opp ^2 = 225 -169

opp ^2 =56

Taking the square root of each side

sqrt( opp^2) = sqrt(56)

opp = sqrt(4 * 14)

opp = 2 sqrt(14)

Since we are in the third quadrant opp is negative

opp = -2 sqrt(14)

We know

sin theta = opp / hyp

sin theta = -2 sqrt(14)/15