Question

Point D is 8 units away from the origin along the x-axis, and is 6 units away along the y-axis. Which of the following could be the coordinates of Point D

Answer 1

The distance between two points (x₁, y₁) and (x₂, y₂) is given by:

`d = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

Now we know that point D, which we can write as (x, y), is at a distance of 8 units from the origin.

Where the origin is written as (0, 0)

We also know that point D is 6 units away along the y-axis.

Then point D could be:

(x, 6)

or

(x, -6)

Now, let's find the x-value for each case, we need to solve:

`8 = √((x - 0)^2 + (\pm6 - 0)^2)`

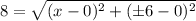
notice that because we have an even power, we will get the same value of x, regardless of which y value we choose.

`8 = √(x^2 + 36) \\\\8^2 = x^2 + 36\\64 - 36 = x^2\\28 = x^2\\\pm√(28) = x\\\pm 5.29 = x`

So we have two possible values of x.

x = 5.29

and

x = -5.29

Then the points that are at a distance of 8 units from the origin, and that are 6 units away along the y-axis are:

(5.29, 6)

(5.29, -6)

(-5.29, 6)

(-5.29, -6)