Answer:
The distance between two points (x₁, y₁) and (x₂, y₂) is given by:
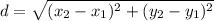
Now we know that point D, which we can write as (x, y), is at a distance of 8 units from the origin.
Where the origin is written as (0, 0)
We also know that point D is 6 units away along the y-axis.
Then point D could be:
(x, 6)
or
(x, -6)
Now, let's find the x-value for each case, we need to solve:
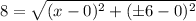
notice that because we have an even power, we will get the same value of x, regardless of which y value we choose.
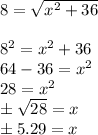
So we have two possible values of x.
x = 5.29
and
x = -5.29
Then the points that are at a distance of 8 units from the origin, and that are 6 units away along the y-axis are:
(5.29, 6)
(5.29, -6)
(-5.29, 6)
(-5.29, -6)