Question

Write the slope-intercept form of the equation of the line described. Through (-1,-1) parallel to y=6x-2

Answer 1

`\boxed {\boxed {\sf y= 6x+5}}`

Explanation:

We are asked to find the slope-intercept equation of a line. Slope-intercept form is one way to write the equation of a line. It is:

`y=mx+b`

Where m is the slope and b is the y-intercept.

We are given a point (-1, -1) and the line is parallel to the line y= 6x-2. Since the line is parallel to the other line, they have the same slope, which is 6. We have a point and a slope, so we should use the point-slope formula to find the equation of the line.

`y-y_1= m (x-x_1)`

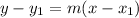
Here, m is the slope and (x₁, y₁) is the point. We know the slope is 6 and the point is (-1, -1). Therefore:

• m= 6
• x₁= -1
• y₁= -1

Substitute the values into the formula.

`y- -1 = 6(x- -1) \\y+1= 6(x+1)`

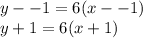
Distribute the 6. Multiply each value inside the parentheses by 6.

`y+1 = (6*x)+ (6*1) \\y+1= 6x+6`

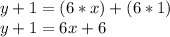
Slope-intercept form requires y to be isolated. 1 is being added to y. The inverse of addition is subtraction. Subtract 1 from both sides.

`y+1-1=6x+6-1 \\y= 6x+5`

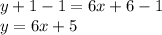
The equation of the line in slope-intercept form is y=6x+5