Question

The impeller shaft of a fluid agitator transmits 20 kW at 430 rpm. If the allowable shear stress in the impeller shaft must be limited to 65 MPa, determine (a) the minimum diameter required for a solid impeller shaft. (b) the maximum inside diameter permitted for a hollow impeller shaft if the outside diameter is 36 mm. (c) the percent savings in weight realized if the hollow shaft is used instead of the solid shaft. (Hint: The weight of a shaft is proportional to its cross-sectional area.)

Answer 1

Given :

Power, P = 20 kW

Speed, N = 430 rpm

Allowable shear stress, τ = 65 MPa

Torque in the shaft is given by :

`$P=(2 \pi NT)/(60)$`

`$T=(60 * 20 * 10^3)/(2 \pi * 430)$`

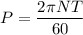
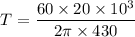
T = 444.37 N.m

Diameter of the solid shaft is

`$d=\sqrt[3]{(16 T)/(\pi \tau)}`

`$d=\sqrt[3]{(16 * 444.37)/(3.14 * 65)}`

`$d=\sqrt[3]{34.83} $`

d = 3.265 m

d = 326.5 mm

Internal diameter of the hollow shaft is :

`$(T)/((\pi)/(32) \left( d_0^4 - d_i^4 \right))=(\tau)/(d_0/2)$`

`$(444.37)/((3.14)/(32) \left( 0.036^4 - d_i^4 \right))=(65 * 10^6)/(0.036/2)$`

`$(444.37)/(0.09 \left( 1.6 * 10^(-6) - d_i^4 \right))=(65 * 10^6)/(0.018)$`

`$(7.99)/( \left( 1.6 * 10^(-6) - d_i^4 \right))=5850000$`

`$1.3* 10^(-6) = 1.6 * 10^(-6) - d_i^4 \right)}$`

`$d_i^4=300000$`

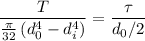
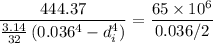
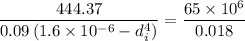
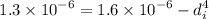
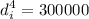
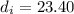`$d_i = 23.40$` mm

Percentage savings in the weight is given by :

Percentage saving =
`$(W_(solid)-W_(hollow))/(W_(solid))*100$`

`$=(V_(solid)-V_(hollow))/(V_(solid))*100$`

`$=(d^2 - (d_0^2 - d_i^2))/(d^2) * 100$`

`$=((326.5)^2 - (0.036^2 - (32.40)^2))/((326.5)^2) * 100$`

`$=(106602 - \left(1.29 * 10^(-3) - 1049.76 \right))/(106602) * 100$`

`$=(106602 - 1049 )/(106602) * 100$`

`$=(105553 )/(106602) * 100$`

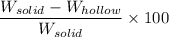
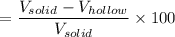
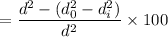
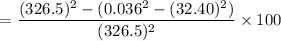
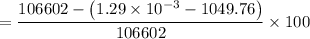
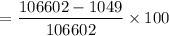
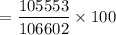
= 99.01 %