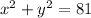Answer:
22.
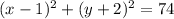
26.
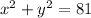
Explanation:
The center of a circle is the midpoint of the diameter.
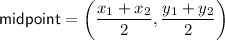
(where
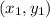 and
and
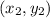 are the endpoints of the diameter)
are the endpoints of the diameter)
The radius of the circle is the distance between the center and an endpoint of the diameter.
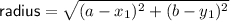
(where
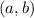 is the center of the circle, and
is the center of the circle, and
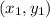 is an endpoint of the diameter)
is an endpoint of the diameter)
The center-radius form of a circle:
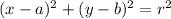
(where (a, b) is the center and r is the radius)
Question 22

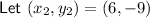
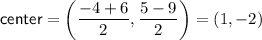

⇒ equation of circle:
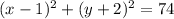
Question 26
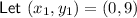
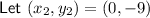

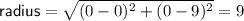
⇒ equation of circle: