Given:
The tens digit of a two digit number is 5 greater the units digit.
If you subtract double the reversed number from it, the result is a fourth of the original number.
To find:
The original number.
Solution:
Let n be the two digit number and x be the unit digit. Then tens digit is (x+5) and the original number is:
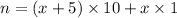
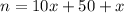
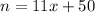
Reversed number is:
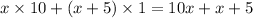
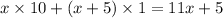
If you subtract double the reversed number from it, the result is a fourth of the original number.
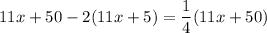
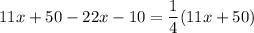
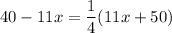
Multiply both sides by 4.

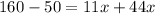
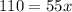
Divide both sides by 55.
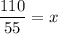
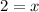
The unit digit is 2. So, the tens digit is
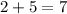 .
.
Therefore, the original number is 72.