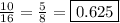Answer:
0.625
Explanation:
Since there are 4 options each time the spinner is spun, there are a total of
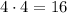 non-distinct sums possible when we spin it twice.
non-distinct sums possible when we spin it twice.
Out of these, the possible sums that meet the condition (less than 6) are 2, 3, 4, and 5 (since the smallest sum possible is 1+1=2).
Count how many ways there are to achieve each of these sums:
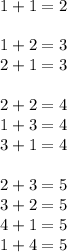
Totally there are 10 ways to achieve a sum less than 6. Therefore, the desired probability is