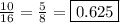Question

A spinner is divided into 4 equal sections numbered 1 through 4. It is spun twice, and the numbers from each spin are added.

What is the probability that the sum is less than 6?

0.563
0.714
0.625
0.750

Answer 1

0.625

Explanation:

Since there are 4 options each time the spinner is spun, there are a total of
`4\cdot 4=16` non-distinct sums possible when we spin it twice.

Out of these, the possible sums that meet the condition (less than 6) are 2, 3, 4, and 5 (since the smallest sum possible is 1+1=2).

Count how many ways there are to achieve each of these sums:

`1+1=2\\\\1+2=3\\2+1=3\\\\2+2=4\\1+3=4\\3+1=4\\\\2+3=5\\3+2=5\\4+1=5\\1+4=5`

Totally there are 10 ways to achieve a sum less than 6. Therefore, the desired probability is
`(10)/(16)=(5)/(8)=\boxed{0.625}`