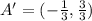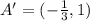Quadrilateral ABCD will be dilated about the origin by a scale factor of 1/3 and then reflected across the y-axis.

Question

asked Feb 19, 2022 146k views

1 Answer

Jonsuh · Answer 1 · 2022-02-22T20:27:29+0000

Answer:

See explanation

Explanation:

The coordinate of ABCD is not given; So, I will solve using general coordinates (x,y).

First, ABCD is dilated by 1/3.

The rule is:

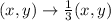
$(x,y) \to (1)/(3)(x,y)$

This gives

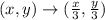
$(x,y) \to ((x)/(3),(y)/(3))$

Next, it is reflected across y-axis.

The rule is:

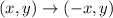
$(x,y) \to (-x,y)$

So, we have:

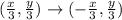
$((x)/(3),(y)/(3)) \to (-(x)/(3),(y)/(3))$

So, the complete transformation is:

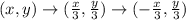
$(x,y) \to ((x)/(3),(y)/(3)) \to (-(x)/(3),(y)/(3))$

Assume that:

A = (1,3)

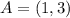
The transformation will be:

A' = (-(1)/(3),(3)/(3))

A' = (-(1)/(3),1)