Answer:
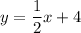
Explanation:
Hi there!
What we need to know:
- Slope-intercept form:
 where m is the slope and b is the y-intercept
where m is the slope and b is the y-intercept - Perpendicular lines always have slopes that are negative reciprocals (examples: 1/2 and -2, 3/4 and -4/3)
1) Determine the slope (m)

Reorganize the given equation into slope-intercept form; subtract 2x from both sides to isolate y:
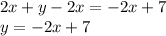
Now, we can easily identify the slope of the line to be -2. Because perpendicular lines always have slopes that are negative reciprocals, the slope of a perpendicular line would be
 . Plug this into
. Plug this into
 :
:
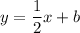
2) Determine the y-intercept (b)
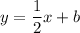
Plug in the given point (2,5) and solve for b:

Subtract 1 from both sides to isolate b:
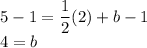
Therefore, the y-intercept of the line is 4. Plug this back into
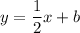 :
:
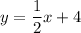
I hope this helps!