Question

A line segment has one endpoint of A (-3,2) and a slope of (-3/5). Find coordinates for B

Answer 1

Explanation:

This is a very interesting problem. We are given the slope and one point, which makes this funner than normal ;)

Filling in the slope formula with what we are given:

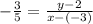`-(3)/(5)=(y-2)/(x-(-3))` which simplifies to

`-(3)/(5)=(y-2)/(x+3)`

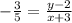
Since slope is rise over run, the rise number is -3; the run number is 5. That means that the equation to find the y coordinate comes from -3 = y - 2; the equation to find the x coordinate comes from 5 = x + 3 (keep in mind that you could have made the x coordinate the negative one; it doesn't matter. You will get the same answer regardless...promise).

Solving for y:

-3 = y - 2 and

y = -1

Solving for x:

5 = x + 3 and

x = 2

Let's check those coordinates in the slope formula and see if our slope is in fact -3/5:

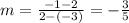`m=(-1-2)/(2-(-3))=-(3)/(5)` so we're all good!

The coordinates of B are (2, -1)