Question

A regular polygon is drawn in a circle so that each vertex is on the circle and is connected to the center by a radius.

Each of the central angles has a measure of 40°. How many sides does the polygon have?
THE
9

Answer 1

Answer is 90 sides

Explanation
(7/2)-2=40
40*2

Answer 2

Answer: 90 sides

Explanation:

Let's say the circle has a center at A and B and C are at the vertices of a polygon. Since this figure is inscribed in a circle, we can draw two radii through the vertices. Because all radii are congruent, we know segment BA is congruent to Segment CA. If a triangle has at least 2 congruent sides, we can identify the triangle as an isosceles triangle. With this we can conclude <ACB is congruent to <ABC. By the definition of congruent angles, m<ACB = M<ABC. Let's say m<ACB = x. By the Triangle Sum Theorem, 40 + x + m<ABC = 180. By substitution, 40 + x + x = 180. When we solve we get x =70. Since radii bisect interior angles we know that each interior angle of this polygon is 140 degrees. If we plug in 140 to our equation,
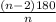`((n-2)180)/(n)` where n is the number of sides, we get n = 90. So we can conclude this polygon has 90 sides