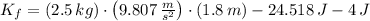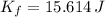Answer:
a) Nonconservative Work

Final Gravitational Potential Energy

Final Translational Energy
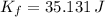
b) Nonconservative Work
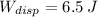
Final Gravitational Potential Energy
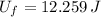
Final Translational Energy
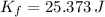
c) Nonconservative Work

Final Gravitational Potential Energy
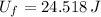
Final Translational Energy
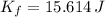
Step-by-step explanation:
The nonconservative work due to water resistance is defined by definition of work:
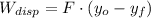 (1)
(1)
Where:
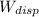 - Dissipate work, in joules.
- Dissipate work, in joules.
 - Resistance force, in newtons.
- Resistance force, in newtons.
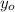 - Initial height, in meters.
- Initial height, in meters.
 - Final height, in meters.
- Final height, in meters.
The final gravitational potential energy (
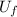 ), in joules, is calculated by means of the definition of gravitational potential energy:
), in joules, is calculated by means of the definition of gravitational potential energy:
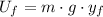 (2)
(2)
Where:
 - Mass of the rock, in kilograms.
- Mass of the rock, in kilograms.
 - Gravitational acceleration, in meters per square second.
- Gravitational acceleration, in meters per square second.
The final translational kinetic energy (
 ), in joules, is obtained by means of the Principle of Energy Conservation, Work-Energy Theorem and definitions of gravitational potential energy and translational kinetic energy:
), in joules, is obtained by means of the Principle of Energy Conservation, Work-Energy Theorem and definitions of gravitational potential energy and translational kinetic energy:
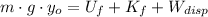 (3)
(3)
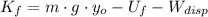
Lastly, the mechanical energy of the system (
 ), in joules, is the sum of final gravitational potential energy, translational kinetic energy and dissipated work due to water resistance:
), in joules, is the sum of final gravitational potential energy, translational kinetic energy and dissipated work due to water resistance:
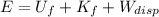 (4)
(4)
Now we proceed to solve the exercise in each case:
a) Nonconservative Work (
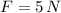 ,
,
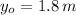 ,
,
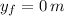 )
)
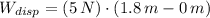

Final Gravitational Potential Energy (
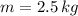 ,
,
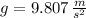 ,
,
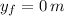 )
)
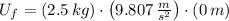

Final Translational Energy (
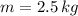 ,
,
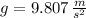 ,
,
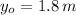 ,
,
 ,
,
 )
)
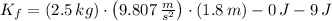
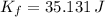
b) Nonconservative Work (
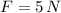 ,
,
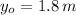 ,
,
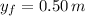 )
)
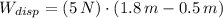
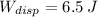
Final Gravitational Potential Energy (
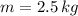 ,
,
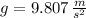 ,
,
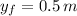 )
)
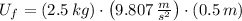
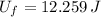
Final Translational Energy (
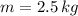 ,
,
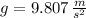 ,
,
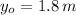 ,
,
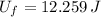 ,
,
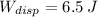 )
)
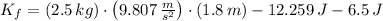
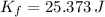
c) Nonconservative Work (
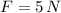 ,
,
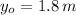 ,
,
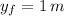 )
)
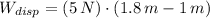

Final Gravitational Potential Energy (
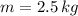 ,
,
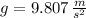 ,
,
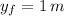 )
)
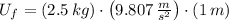
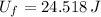
Final Translational Energy (
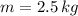 ,
,
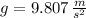 ,
,
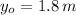 ,
,
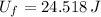 ,
,
 )
)