Answer:
θ' = 14.44 ×
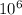
Step-by-step explanation:
given data
total distance is d = 4820
radius = 1.4 cm
solution
we get here total angle by which the wheel rotates traveling is express as
⇒
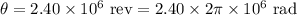 ................1
................1
and
total angle (θ) and the total distance (d) express as
⇒ d = r × θ ...............2
here r is radius
and here rotated through some other angle θ' so put value in given equation and find revolutions
⇒ d = (r+r)θ' ........3
here r = d/θ
so
⇒
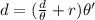
so put value and get θ'
⇒ θ' = 2.40 × 2π ×
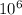 ×
×
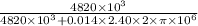
⇒ θ' = 14.44 ×
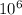 rev
rev