Question

A physical pendulum in the form of a planar object moves in simple harmonic motion with a frequency of 0.680 Hz. The pendulum has a mass of 2.00 kg, and the pivot is located 0.340 m from the center of mass. Determine the moment of inertia of the pendulum about the pivot point.

Answer 1

Therefore, the moment of inertia is:

`I=0.37 \: kgm^(2)`

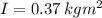
Step-by-step explanation:

The period of an oscillation equation of a solid pendulum is given by:

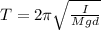`T=2\pi \sqrt{(I)/(Mgd)}` (1)

Where:

• I is the moment of inertia
• M is the mass of the pendulum
• d is the distance from the center of mass to the pivot
• g is the gravity

Let's solve the equation (1) for I

`T=2\pi \sqrt{(I)/(Mgd)}`

`I=Mgd((T)/(2\pi))^(2)`

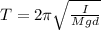
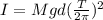
Before find I, we need to remember that

`T = (1)/(f)=(1)/(0.680)=1.47\: s`

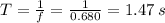
Now, the moment of inertia will be:

`I=2*9.81*0.340((1.47)/(2\pi))^(2)`

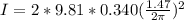
Therefore, the moment of inertia is:

`I=0.37 \: kgm^(2)`

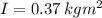
I hope it helps you!