Complete Question
A manufacturer of nickel-hydrogen batteries randomly selects 100 nickel plates for test cells, cycles them a specified number of times, and determines that 11 of the plates have blistered. Does this provide compelling evidence for concluding that more than 10% of plates blister under such circumstances?
A) State H_0 and H_a, (5 pts)
B) Test the hypothesis using the P-Value approach at a significance level of 4%: (15 pts)
Expert Answer
Answer:
a)
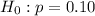
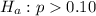
b) We fail to reject Null hypothesis
Explanation:
From the question we are told that:
Sample size n=100
No. with blistered x=11
a)
Generally the Hypothesis given as
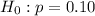
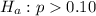
b)
Since p=0.10
Therefore
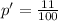
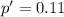
Test statistics
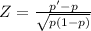
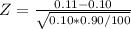
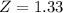
From table
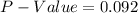
Therefore
P-value >0.04 significance level
Hence,We cannot conclude that at
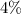 significance level the proportion is greater than
significance level the proportion is greater than
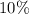
We fail to reject Null hypothesis