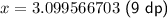Question

Find the zeros


`\\ \rm\Rrightarrow 4x^3-15x^2+10x-6=0`

Note:-

Make sure you include all steps.

Proper explanation is mandatory .


Spams/irrelevant/wrong/copied answers will be deleted on the spot so don't waste your precious time here by spamming .

Instead provide good explanation and correct answer​

Answer 1

`x=3.099566703 \textsf{ (9 dp)}`

Explanation:

Newton-Rhapson method

This iterative method finds roots of equations in the form f(x) = 0 when an equation cannot be solved using the usual analytical methods

This method works by finding the tangent to a function at a point
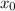`x_0`, and using its x-intercept for the next iteration,
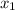`x_1`. Repeating the process iteratively gets you closer to the root.

Newton-Rhapson formula

`x_(n+1)=x_n-(f(x_n))/(f'(x_n))`

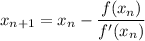
Given function:

`f(x)=4x^3-15x^2+10x-6=0`

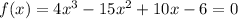
First check that the function is in the form f(x) = 0 ← yes!

(if it is not, rearrange it so that it is equal to zero)

Now differentiate the function:

`f'(x)=12x^2-30x+10`

Substitute the function and its derivative into the N-R formula:

`x_(n+1)=x_n-\frac{4{x_n}^3-15{x_n}^2+10{x_n}-6}{12{x_n}^2-30{x_n}+10}`

To determine which value to set as
`x_0` examine the function.

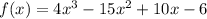`f(x)=4x^3-15x^2+10x-6` is a cubic function with a positive leading coefficient.

Therefore, its endpoint behavior is:

`f(x) \rightarrow \infty \textsf{ as } x \rightarrow \infty\\f(x) \rightarrow -\infty \textsf{ as } x \rightarrow -\infty`

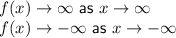
Its y-intercept is (0, -6)

It's turning points are when
`f'(x)=0`

Therefore, using the quadratic formula, its turning points are:

`x=(-(-30)\pm√((-30)^2-4(12)(10)))/(2(12))=(15\pm√(105))/(12)`

Sketching the graph (see attached) suggests that the x-intercept will be when:

`x > (15+√(105))/(12)`

`\implies x > 2.1039...`

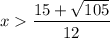
Let's start with inputting values of x = 3 and x = 4 into the function:

`f(3)=4(3)^3-15(3)^2+10(3)-6=-3\\f(4)=4(4)^3-15(4)^2+10(4)-6=50`

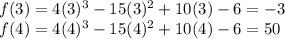
The x-intercept will be between values where there is a change in sign. As there is a change in sign between f(3) and f(4), the root is
`3 < x < 4`

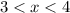
Therefore, let
`x_0=3`

`\implies x_(1)=x_0-\frac{4{x_0}^3-15{x_0}^2+10{x_0}-6}{12{x_0}^2-30{x_0}+10}`

`\implies x_(1)=3-(4(3)^3-15(3)^2+10(3)-6)/(12(3)^2-30(3)+10)=(87)/(28)`

`\implies x_(2)=x_1-\frac{4{x_1}^3-15{x_1}^2+10{x_1}-6}{12{x_1}^2-30{x_1}+10}=3.099605842...`

`\implies x_(3)=x_2-\frac{4{x_2}^3-15{x_2}^2+10{x_2}-6}{12{x_2}^2-30{x_2}+10}=3.099566704...`

`\implies x_(4)=x_3-\frac{4{x_3}^3-15{x_3}^2+10{x_3}-6}{12{x_3}^2-30{x_3}+10}=3.099566703...`

`\implies x_(5)=x_4-\frac{4{x_4}^3-15{x_4}^2+10{x_4}-6}{12{x_4}^2-30{x_4}+10}=3.099566703...`

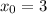
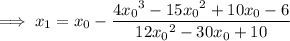
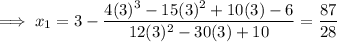
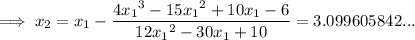
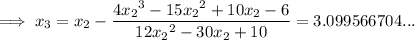
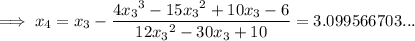
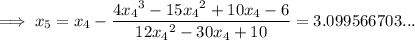
Therefore,
`x=3.099566703 \textsf{ (9 dp)}`