Answer:
The company should use a mean of 12.37 ounces.
Explanation:
Normal Probability Distribution
Problems of normal distributions can be solved using the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the z-score of a measure X is given by:
, the z-score of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
The distribution for the amount of beer dispensed by the machine follows a normal distribution with a standard deviation of 0.17 ounce.
This means that
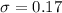
The company can control the mean amount of beer dispensed by the machine. What value of the mean should the company use if it wants to guarantee that 98.5% of the bottles contain at least 12 ounces (the amount on the label)?
This is
 , considering that when
, considering that when
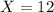 , Z has a p-value of
, Z has a p-value of
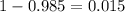 , so when
, so when
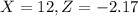 .
.
Then

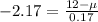
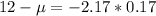
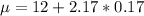

The company should use a mean of 12.37 ounces.