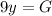Answer:
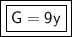
Explanation:
We are given the following equation and asked to find the missing factor that makes the equality true.
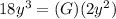
Essentially, we need to solve for the variable G.
1. Factoring
One method we can use is factoring.
We could factor the expression 18y³ because we know one factor is 2y². Since this is one of the factors, the other must be 9y.
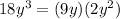
If we compare this factored version of the expression with the original equation we see that 9y and G correspond, so they must be equal.
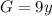
2. Solving
Another method we could use is solving.
We can solve the original equation for G by isolating the variable.
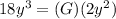
G is being multiplied by 2y³. The inverse of multiplication is division, so we divide both sides of the equation by 2y³.
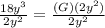
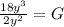
The coefficients are divided as usual and the exponents are subtracted.