Question

Help with 4b thank you. ​

Answer 1

First let's compute dx/dt

`x = t - (1)/(t)\\\\x = t - t^(-1)\\\\(dx)/(dt) = (d)/(dt)\left(t - t^(-1)\right)\\\\(dx)/(dt) = 1-(-1)t^(-2)\\\\(dx)/(dt) = 1+(1)/(t^(2))\\\\(dx)/(dt) = (t^2)/(t^(2))+(1)/(t^(2))\\\\(dx)/(dt) = (t^2+1)/(t^(2))\\\\`

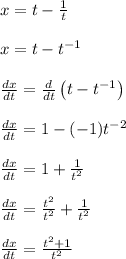
Now compute dy/dt

`y = 2t + (1)/(t)\\\\y = 2t + t^(-1)\\\\(dy)/(dt) = (d)/(dt)\left(2t + t^(-1)\right)\\\\(dy)/(dt) = 2 - t^(-2)\\\\(dy)/(dt) = 2 - (1)/(t^2)\\\\(dy)/(dt) = (2t^2)/(t^2)-(1)/(t^2)\\\\(dy)/(dt) = (2t^2-1)/(t^2)\\\\`

From here, apply the chain rule to say

`(dy)/(dx) = (dy*dt)/(dx*dt)\\\\(dy)/(dx) = (dy)/(dt) * (dt)/(dx)\\\\(dy)/(dx) = (dy)/(dt) / (dx)/(dt)\\\\(dy)/(dx) = (2t^2-1)/(t^2) / (t^2+1)/(t^(2))\\\\(dy)/(dx) = (2t^2-1)/(t^2) * (t^(2))/(t^2+1)\\\\(dy)/(dx) = (2t^2-1)/(t^2+1)\\\\`

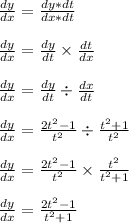
We could use polynomial long division, or we could add 2 and subtract 2 from the numerator and do a bit of algebra like so

`(dy)/(dx) = (2t^2-1)/(t^2+1)\\\\(dy)/(dx) = (2t^2-1+2-2)/(t^2+1)\\\\(dy)/(dx) = ((2t^2+2)-1-2)/(t^2+1)\\\\(dy)/(dx) = (2(t^2+1)-3)/(t^2+1)\\\\(dy)/(dx) = (2(t^2+1))/(t^2+1)-(3)/(t^2+1)\\\\(dy)/(dx) = 2-(3)/(t^2+1)\\\\`

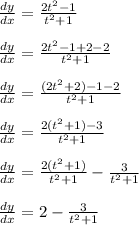
This concludes the first part of 4b

=======================================================

Now onto the second part.

Since t is nonzero, this means either t > 0 or t < 0.

If t > 0, then,

`t > 0\\\\t^2 > 0\\\\t^2+1 > 1\\\\(1)/(t^2+1) < 1 \ \text{ ... inequality sign flip}\\\\(3)/(t^2+1) < 3\\\\-(3)/(t^2+1) > -3 \ \text{ ... inequality sign flip}\\\\-(3)/(t^2+1)+2 > -3 + 2\\\\2-(3)/(t^2+1) > -1\\\\-1 < 2-(3)/(t^2+1)\\\\-1 < (dy)/(dx)\\\\`

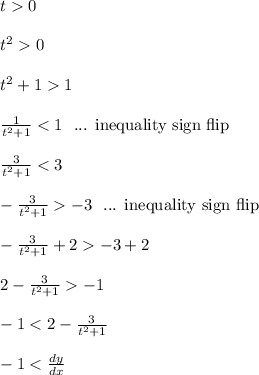
note the inequality signs flipping when we apply the reciprocal to both sides, and when we multiply both sides by a negative value.

You should find that the same conclusion happens when we consider t < 0. Why? Because t < 0 becomes t^2 > 0 after we square both sides. The steps are the same as shown above.

So both t > 0 and t < 0 lead to
`-1 < (dy)/(dx)`

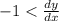
We can say that -1 is the lower bound of dy/dx. It never reaches -1 itself because t = 0 is not allowed.

We could say that

`\displaystyle \lim_(t\to0)\left(2-(3)/(t^2+1)\right)=-1\\\\`

---------------------------------------

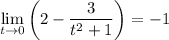
To establish the upper bound, we consider what happens when t approaches either infinity.

If t approaches positive infinity, then,

`\displaystyle L = \lim_(t\to\infty)\left(2-(3)/(t^2+1)\right)\\\\\\\displaystyle L = \lim_(t\to\infty)\left((2t^2-1)/(t^2+1)\right)\\\\\\\displaystyle L = \lim_(t\to\infty)\left((2-(1)/(t^2))/(1+(1)/(t^2))\right)\\\\\\\displaystyle L = (2-0)/(1+0)\\\\\\\displaystyle L = 2\\\\`

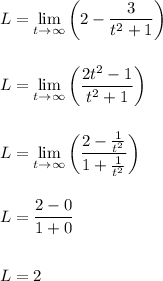
As t approaches infinity, the dy/dx value approaches L = 2 from below.

The same applies when t approaches negative infinity.

So we see that
`(dy)/(dx) < 2`

---------------------------------------

Since
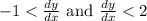`-1 < (dy)/(dx) \text{ and } (dy)/(dx) < 2`, those two inequalities combine into the compound inequality
`-1 < (dy)/(dx) < 2`

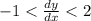
So dy/dx is bounded between -1 and 2, exclusive of either endpoint.