Question

For all of the Following use the function LaTeX: P\left(x\right)\:=\:\left(x+3\right)^2+2 . My original vertex is

Answer 1

A) Q(x) = (x + 3)² + 5, and the vertex is (-3, 5)

B) R(x) = (x - 3)² + 2, and the vertex is (3, 2)

C) S(x) = (x - 1)² - 5, and the vertex is (1, -5)

Explanation:

The given function is P(x) = (x + 3)² + 2

The given function is a parabolic function in vertex form, f(x) = a·(x - h)² + k, and vertex, (h, k)

By comparison, the vertex of the function P(x) = (x + 3)² + 2 is (-3, 2)

A) A function f(x) translated α units UP gives

f(x) (translated α units UP) → f(x) + α

A translation of the function 3 units UP is given by adding 3 to the given function as follows;

Q(x) = P(x) + 3

∴ Q(x) = (x + 3)² + 2 + 3 = (x + 3)² + 5

Q(x) = (x + 3)² + 5, and the vertex by comparison to f(x) = a·(x - h)² + k, and vertex, (h, k) is (-3, 5)

B) A function f(x) translated b units RIGHT gives;

f(x) translated b units right → f(x - b)

∴ P(x) = (x + 3)² + 2 translated 6 units RIGHT gives;

P(x) = (x + 3)² + 2 (translated 6 units RIGHT) → R(x) = (x + 3 - 6)² + 2 = (x - 3)² + 2

R(x) = (x - 3)² + 2, and the vertex by comparison is (3, 2)

C) A function translated α units DOWN and b units RIGHT is given as follows;

`f(x) \ translated \ by\ \dbinom{b}{a} \rightarrow f(x - b) - a`

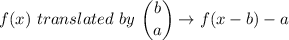
Therefore, the given function, P(x) = (x + 3)² + 2, translated 7 units DOWN and 4 units RIGHT gives;

`P(x) = (x + 3)^2 + 5 \ translated \ by\ \dbinom{4}{-7} \rightarrow P(x - 4) - 7 = S(x)`

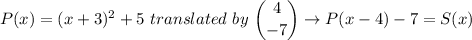
S(x) = P(x - 4) - 7 = (x + 3 - 4)² + 2 - 7 = (x - 1)² - 5

`P(x) = (x + 3)^2 + 5 \ translated \ by\ \dbinom{4}{-7} \rightarrow (x - 1)^2 - 5= S(x)`

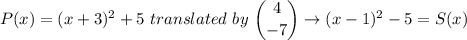
S(x) = (x - 1)² - 5, and the vertex by comparison is (1, -5)