Answer:
A) Q(x) = (x + 3)² + 5, and the vertex is (-3, 5)
B) R(x) = (x - 3)² + 2, and the vertex is (3, 2)
C) S(x) = (x - 1)² - 5, and the vertex is (1, -5)
Explanation:
The given function is P(x) = (x + 3)² + 2
The given function is a parabolic function in vertex form, f(x) = a·(x - h)² + k, and vertex, (h, k)
By comparison, the vertex of the function P(x) = (x + 3)² + 2 is (-3, 2)
A) A function f(x) translated α units UP gives
f(x) (translated α units UP) → f(x) + α
A translation of the function 3 units UP is given by adding 3 to the given function as follows;
Q(x) = P(x) + 3
∴ Q(x) = (x + 3)² + 2 + 3 = (x + 3)² + 5
Q(x) = (x + 3)² + 5, and the vertex by comparison to f(x) = a·(x - h)² + k, and vertex, (h, k) is (-3, 5)
B) A function f(x) translated b units RIGHT gives;
f(x) translated b units right → f(x - b)
∴ P(x) = (x + 3)² + 2 translated 6 units RIGHT gives;
P(x) = (x + 3)² + 2 (translated 6 units RIGHT) → R(x) = (x + 3 - 6)² + 2 = (x - 3)² + 2
R(x) = (x - 3)² + 2, and the vertex by comparison is (3, 2)
C) A function translated α units DOWN and b units RIGHT is given as follows;
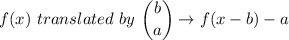
Therefore, the given function, P(x) = (x + 3)² + 2, translated 7 units DOWN and 4 units RIGHT gives;
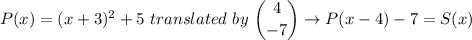
S(x) = P(x - 4) - 7 = (x + 3 - 4)² + 2 - 7 = (x - 1)² - 5
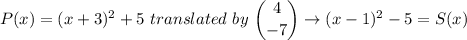
S(x) = (x - 1)² - 5, and the vertex by comparison is (1, -5)