Answer:
a) The 95% confidence interval for the mean mpg, for the certain model of car is (23.3, 30.1). This means that we are 95% sure that the true mean mpg of the model of the car is between 23.3 mpg and 30.1 mpg.
b) Increasing the confidence level, the value of T would increase, thus increasing the margin of error and making the interval wider.
c) 37 cars would have to be sampled.
Explanation:
Question a:
We have the sample standard deviation, and thus, the t-distribution is used to solve this question.
The first step to solve this problem is finding how many degrees of freedom, we have. This is the sample size subtracted by 1. So
df = 15 - 1 = 14
95% confidence interval
Now, we have to find a value of T, which is found looking at the t table, with 14 degrees of freedom(y-axis) and a confidence level of
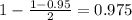 . So we have T = 2.1448
. So we have T = 2.1448
The margin of error is:
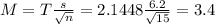
In which s is the standard deviation of the sample and n is the size of the sample.
The lower end of the interval is the sample mean subtracted by M. So it is 26.7 - 3.4 = 23.3 mpg.
The upper end of the interval is the sample mean added to M. So it is 26.7 + 3.4 = 30.1 mpg.
The 95% confidence interval for the mean mpg, for the certain model of car is (23.3, 30.1). This means that we are 95% sure that the true mean mpg of the model of the car is between 23.3 mpg and 30.1 mpg.
b. What would happen to the interval if you increased the confidence level from 95% to 99%? Explain
Increasing the confidence level, the value of T would increase, thus increasing the margin of error and making the interval wider.
c. The lead engineer is not happy with the interval you constructed and would like to keep the width of the whole interval to be less than 4 mpg wide. How many cars would you have to sample to create the interval the engineer is requesting?
Width is twice the margin of error, so a margin of error of 2 would be need. To solve this, we have to consider the population standard deviation as
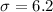 , and then use the z-distribution.
, and then use the z-distribution.
We have that to find our
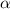 level, that is the subtraction of 1 by the confidence interval divided by 2. So:
level, that is the subtraction of 1 by the confidence interval divided by 2. So:
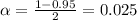
Now, we have to find z in the Z-table as such z has a p-value of
 .
.
That is z with a pvalue of
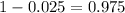 , so Z = 1.96.
, so Z = 1.96.
Now, find the margin of error M as such
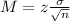
In which
 is the standard deviation of the population and n is the size of the sample.
is the standard deviation of the population and n is the size of the sample.
How many cars would you have to sample to create the interval the engineer is requesting?
This is n for which M = 2. So
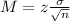
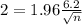
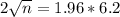
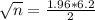
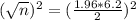
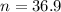
Rounding up:
37 cars would have to be sampled.