Question

Select all the statements that are true for the following systems of equations

Answer 1

A. System C simplifies to 2x - 3y = 4 and 4x - y = 54 by dividing the second equation by three (3).

B. Systems A and C have the same solutions.

C. Systems A and B have different solutions.

Explanation:

Given the following system of equations;

System A

2x - 3y = 4 .....equation 1

4x - y = 18 .......equation 2

We would solve the above equations using the elimination method;

Multiplying eqn 1 by 2;

2*(2x) - 2*(3y) = 4*2

4x - 6y = 8 ...... equation 3

Subtracting eqn 2 from eqn 3;

(4x - 4x) + (-6y - (-y)) = 8 - 18

0 + (-6y + y) = -10

-5y = -10

5y = 10

`y = \frac {10}{5}`

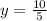
y = 2

To find the value of x;

2x - 3y = 4

2x - 3(2) = 4

2x - 6 = 4

2x = 4 + 6

2x = 10

`x = \frac {10}{2}`

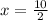
x = 5

Solutions (x, y) = (5, 2)

System B

3x - 4y = 5 ..... equation 1

y = 5x + 3 ..... equation 2

We would solve the equations using substitution method;

Substituting eqn 2 into eqn 1, we have;

3x - 4(5x + 3) = 5

3x - 20x - 12 = 5

-17x - 12 = 5

-17x = 12 + 5

-17x = 17

`x = \frac {-17}{17}`

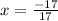
x = -1

To find the value of y;

y = 5x + 3

y = 5(-1) + 3

y = -5 + 3

y = -2

Solutions (x, y) = (-1, -2)

System C

2x - 3y = 4 ..... equation 1

12x - 3y = 54 ...... equation 2

We would solve the above equations using the elimination method;

Subtracting eqn 2 from eqn 1;

(2x - 12x) + (-3y -(-3y)) = 4 - 54

-10x + (-3y + 3y) = -50

-10x + 0 = -50

-10x = -50

10x = 50

`x = \frac {50}{10}`

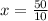
x = 5

To find the value of y;

2x - 3y = 4

2(5) - 3y = 4

10 - 3y = 4

3y = 10 - 4

3y = 6

`y = \frac {6}{3}`

y = 2

Solutions (x, y) = (5, 2)