Answer:
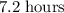 .
.
Explanation:
Let the volume of this cistern be
 .
.
The first pipe fills the cistern at a rate of
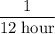 .
.
In other words, each hour, the first pipe would fill
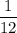 of the cistern every hour.
of the cistern every hour.
On the other hand, the second pipe fills the cistern at a rate of
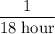 .
.
This pipe would fill
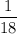 of the cistern every hour.
of the cistern every hour.
Hence, when opened together, the two pipes would fill
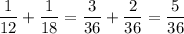 of this cistern every hour.
of this cistern every hour.
At this rate, it would take
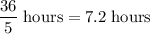 for the two pipes to fill the entire cistern.
for the two pipes to fill the entire cistern.