Answer:
The spring constant of the spring is 10.3 N/m.
Step-by-step explanation:
Given that,
Mass of a bungee jumper, m = 59 kg
The period of oscillation, T = 0.25 min = 15 sec
We need to find the spring constant of the bungee cord. We know that the period of oscillation is given by :
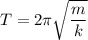
Where
k is the spring constant
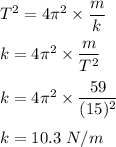
So, the spring constant of the spring is 10.3 N/m.