Answer:
Explanation:
The position function for this is given as
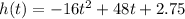 where h(t) is the height of the football at any time t. If the ball is caught at 5.25 feet, that h(t) value is 5.25 since we are looking for the time the ball was in the air from its initial 2.75 feet to 5.25 feet, when it was caught.
where h(t) is the height of the football at any time t. If the ball is caught at 5.25 feet, that h(t) value is 5.25 since we are looking for the time the ball was in the air from its initial 2.75 feet to 5.25 feet, when it was caught.
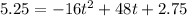 and set this equal to 0:
and set this equal to 0:
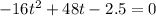 and factor.
and factor.
When we factor we get
t = .05 and t = 2.95 in seconds.
That first time tell us how long it takes to go from the initial height of 2.75 to a point 2.5 feet higher, 5.25. To get get back down to the 5.25 foot height on the other side of the vertex, is 2.95 seconds. So the total time the ball was in the air was 3 seconds exactly.