Answer:
a) 0.321 = 32.1% probability of obtaining a negative daily return, on any given day.
b) 0.103 = 10.3% probability of having a negative daily return for two days in a row.
c) (-$1449.68, $3109.68)
d) A bonus of $4,488.174 is needed.
Explanation:
Normal Probability Distribution
Problems of normal distributions can be solved using the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the z-score of a measure X is given by:
, the z-score of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Normal distribution with mean = $830 and standard deviation = $1,781.
This means that
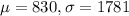
(a) What is the probability of obtaining a negative daily return, on any given day?
This is the p-value of Z when X = 0, so:

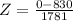
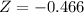
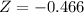 has a p-value 0.321.
has a p-value 0.321.
0.321 = 32.1% probability of obtaining a negative daily return, on any given day.
(b) Assuming the returns on successive days are independent of each other, what is the probability of having a negative daily return for two days in a row?
Each day, 0.3206 probability, so:
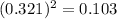
0.103 = 10.3% probability of having a negative daily return for two days in a row.
(c) Give the boundaries of the interval containing the middle 80% of daily returns
Between the 50 - (80/2) = 10th percentile and the 50 + (80/2) = 90th percentile.
10th percentile:
X when Z has a p-value of 0.1, so X when Z = -1.28.

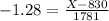
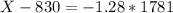

90th percentile:
X when Z has a p-value of 0.9, so X when Z = 1.28.

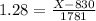


So
(-$1449.68, $3109.68)
d) As part of its incentive program, any trader who obtains a daily return in the top 2% of historical returns receives a special bonus. What daily return is needed to get this bonus?
The 100 - 2 = 98th percentile, which is X when Z has a p-value of 0.98, so X when Z = 2.054.

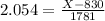
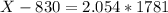
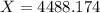
A bonus of $4,488.174 is needed.