Question

Determine the number of roots the equation x^2+14x=-49 using the discriminant.

Answer 1

`\boxed {\boxed {\sf 1 \ real \ root}}`

Explanation:

The quadratic formula is used to find the roots or zeroes of a quadratic equation. It is:

`x=\frac{-b\pm \sqrt{{{b}^(2)}-4ac}}{2a}`

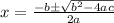
The discriminant helps us find the number of roots. If the discriminant is...

• Negative: there are no real roots
• Zero: there is one real root
• Positive: there are two real roots

It is the expression under the square root symbol:

`b^2-4ac`

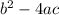
First, we must put the given quadratic equation into standard form, which is:

`ax^2+bx+c=0`

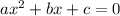
The equation given is
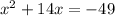`x^2 +14x= -49`. We have to move the -49 to the left side. Since it is a negative number, we add 49 to both sides.

`x^2+14x+49 = -49 +49 \\x^2+14x+49=0`

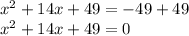
Now we can solve for the discriminant because we know that:

• a= 1
• b= 14
• c= 49

Substitute these values into the formula for the discriminant.

`(14)^2 -4 (1)(49)`

Solve according to PEMDAS: Parentheses, Exponents, Multiplication, Division, Addition, Subtraction.

Solve the exponent.

• (14)²= 14 * 14= 196

`196- 4(1)(49)`

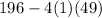
Multiply 4, 1, and 49.

`196-196`

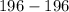
Subtract.

`0`

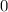
The discriminant is zero, so the quadratic equation x²+ 14x = -49 has 1 real root.