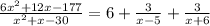Question

Find the partial fraction decomposition of the improper rational expression (6x^(2)+12x-177)/(x^(2)+x-30)

Answer 1

Answer: the closest answer is 6+3/x+3/x-5

Explanation:

Answer 2

`(6x^2+12x-177)/(x^2+x -30)=6+(3)/(x-5)+(3)/(x+6)`

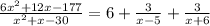
Explanation:

From the question we are told that:

Partial fraction is given as

`((6x^2+12x-177))/((x^2+x-30))`

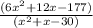
Factorized

`6+(6x+3)/(x^2+x−30)`

`(6x+3)/((x-5)(x+6))`

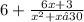
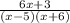
Generally the equation for Partial Fraction is mathematically given by

`(6x+3)/((x-5)(x+6))=(A)/(x-5)+(B)/(x+6)`

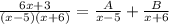
Therefore

`(6x+3)/((x-5)(x+6))=((x-5)B+(x+6)A)/((x-5)(x+6))`

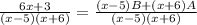
Since denominators are equal

`6x+3=(x-5)B+(x+6)A`

`6x+3=xA+xB+6A-5B`

`6x+3=x(A+B)+6A-5B`

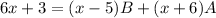
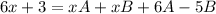
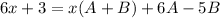
Collecting Coefficients respectively

`A+B=6 .......(equ 1)`

`6A- 5B=3.........(equ 2)`

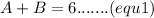
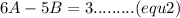
Therefore

A=3

B=3

Hence, Partial fraction decomposition is

`(6x^2+12x-177)/(x^2+x -30)=6+(3)/(x-5)+(3)/(x+6)`