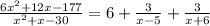Answer:
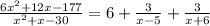
Explanation:
From the question we are told that:
Partial fraction is given as
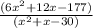
Factorized
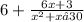
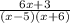
Generally the equation for Partial Fraction is mathematically given by
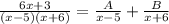
Therefore

Since denominators are equal

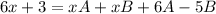
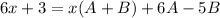
Collecting Coefficients respectively
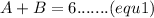
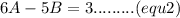
Therefore
A=3
B=3
Hence, Partial fraction decomposition is