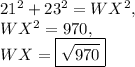Answer:
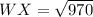
Explanation:
The diagonals of a kite intersect at a 90-degree angle. In this figure, right triangle
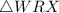 is formed by half of each of the diagonals.
is formed by half of each of the diagonals.
In any right triangle, the Pythagorean Theorem states that
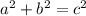 , where
, where
 and
and
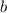 are two legs of the triangle and
are two legs of the triangle and
 is the hypotenuse.
is the hypotenuse.
Segment WR is one leg of the triangle and is given as 21. XR forms the other leg of the triangle, and is exactly half of diagonal XZ. Therefore,
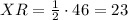 .
.
The segment we're being asking to find, WX, marks the hypotenuse of the triangle.
Therefore, substitute our known information into the Pythagorean Theorem: