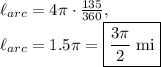Question

Find the circumference of the circle. Then, find the length of each bolded arc. Use appropriate notation

Answer 1

`\text{1) }\\\text{Circumference: }24\pi \text{ m}},\\\text{Length of bolded arc: }18\pi \text{ m}\\\\\text{3)}\\\text{Circumference. }4\pi \text{ mi},\\\text{Length of bolded arc: } (3\pi)/(2)\text{ mi}`

Explanation:

The circumference of a circle with radius
`r` is given by
`C=2\pi r`. The length of an arc is makes up part of this circumference, and is directly proportion to the central angle of the arc. Since there are 360 degrees in a circle, the length of an arc with central angle
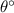`\theta^(\circ)` is equal to
`2\pi r\cdot (\theta)/(360)`.

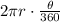Formulas at a glance:

• Circumference of a circle with radius
  `r`:
  `C=2\pi r`
• Length of an arc with central angle
  `\theta^(\circ)`:
  `\ell_(arc)=2\pi r\cdot (\theta)/(360)`

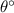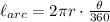
Question 1:

The radius of the circle is 12 m. Therefore, the circumference is:

`C=2\pi r,\\C=2(\pi)(12)=\boxed{24\pi\text{ m}}`

The measure of the central angle of the bolded arc is 270 degrees. Therefore, the measure of the bolded arc is equal to:

`\ell_(arc)=24\pi \cdot (270)/(360),\\\\\ell_(arc)=24\pi \cdot (3)/(4),\\\\\ell_(arc)=\boxed{18\pi\text{ m}}`

Question 2:

In the circle shown, the radius is marked as 2 miles. Substituting
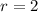`r=2` into our circumference formula, we get:

`C=2(\pi)(2),\\C=\boxed{4\pi\text{ mi}}`

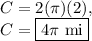
The measure of the central angle of the bolded arc is 135 degrees. Its length must then be:

`\ell_(arc)=4\pi \cdot (135)/(360),\\\ell_(arc)=1.5\pi=\boxed{(3\pi)/(2)\text{ mi}}`