Question

The motion of a particle is defined by the relation x 5 t 3 2 9t 2 1 24t 2 8, where x and t are expressed in inches and seconds, respectively. Determine (a) when the velocity is zero, (b) the position and the total distance traveled when the acceleration is zero.

Answer 1

a) t = 2.0 s, b) x_f = - 24.56 m, Δx = 16.56 m

Step-by-step explanation:

This is an exercise in kinematics, the relationship of position and time is indicated

x = 5 t³ - 9t² -24 t - 8

a) ask when the velocity is zero

speed is defined by

v =
`(dx)/(dt)`

let's perform the derivative

v = 15 t² - 18t - 24

0 = 15 t² - 18t - 24

let's solve the quadratic equation

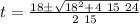
`t = (18 \pm √(18^2 + 4 \ 15 \ 24) )/(2 \ 15)`

t =
`(18 \pm 42)/(30)`

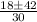
t1 = -0.8 s

t2 = 2.0 s

the time has to be positive therefore the correct answer is t = 2.0 s

b) the position and distance traveled for a = 0

acceleration is defined by

a = dv / dt

a = 30 t - 18

a = 0

30 t = 18

t = 18/30

t = 0.6 s

we substitute this time in the expression of the position

x = 5 0.6³ - 9 0.6² - 24 0.6 - 8

x = 1.08 - 3.24 - 14.4 - 8

x = -24.56 m

we see that all the movement is in one dimension so the distance traveled is the change in position between t = 0 and t = 0.6 s

the position for t = 0

x₀ = -8 m

the position for t = 0.6 s

x_f = - 24.56 m

the distance

ΔX = x_f - x₀

Δx = | -24.56 -(-8) |

Δx = 16.56 m