Question

A small liberal arts college in the Northeast has 300 freshmen. One hundred ten of the freshmen are education majors. Suppose sixty freshmen are randomly selected (without replacement). Find the standard deviation of the number of education majors in the sample.

Answer 1

To find the standard deviation of the number of education majors in the sample, we use the formula for the standard deviation of a sample proportion: σ = √((p*(1-p))/n), where σ is the standard deviation, p is the proportion of education majors in the population, and n is the sample size. Plugging in the values, the standard deviation is approximately 0.0649.

Step-by-step explanation:

To find the standard deviation of the number of education majors in the sample, we need to use the formula for the standard deviation of a sample proportion. The formula is:

• σ = √((p*(1-p))/n)

Where σ is the standard deviation, p is the proportion of education majors in the population, and n is the sample size.

In this case, the proportion of education majors in the population is 110/300 = 0.3667, and the sample size is 60. Plugging these values into the formula, we have:

• σ = √((0.3667*(1-0.3667))/60) = 0.0649

Therefore, the standard deviation of the number of education majors in the sample is approximately 0.0649.

Answer 2

The standard deviation of the number of education majors in the sample is of 3.34.

Step-by-step explanation:

The students are chosen without replacement, which means that the hypergeometric distribution is used to solve this question.

Hypergeometric distribution:

The probability of x successes is given by the following formula:

`P(X = x) = h(x,N,n,k) = (C_(k,x)*C_(N-k,n-x))/(C_(N,n))`

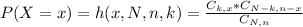
In which:

x is the number of successes.

N is the size of the population.

n is the size of the sample.

k is the total number of desired outcomes.

Combinations formula:

`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

Standard deviation:

The standard deviation of the hypergeometric distribution is:

`\sigma = \sqrt{(nk)/(N)(1 - (k)/(N))((N-n)/(N-1))}`

In this question:

300 freshmen means that
`N = 300`

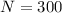
110 are education majors, which means that
`k = 110`

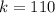
60 are chosen, which means that
`n = 60`

Find the standard deviation of the number of education majors in the sample.

`\sigma = \sqrt{(60*110)/(300)(1 - (110)/(300))((240)/(299))} = 3.34`

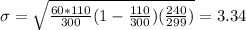
The standard deviation of the number of education majors in the sample is of 3.34.